




 |
|
In our previous interview, you explained the slip coefficient Ks and the flexibility coefficient Km in the basic theoretical formula of expansion amount  . Now, please explain the element Lsin . Now, please explain the element Lsin . If I recall correctly, L is the web's traveling distance per unit time, and . If I recall correctly, L is the web's traveling distance per unit time, and is the inclination angle of an FE roll. Speaking bluntly, it would seem to be a little bit difficult to get a sense of the expansion amount when you use a trigonometric function such as sine... is the inclination angle of an FE roll. Speaking bluntly, it would seem to be a little bit difficult to get a sense of the expansion amount when you use a trigonometric function such as sine... |
|
| Tsuchida: |
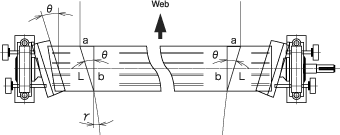
 First, let me explain that the slip coefficient and flexibility coefficient are NOT expressed by a numerical value but are factors to be taken into consideration when discussing the expansion amount. However, the element Lsin First, let me explain that the slip coefficient and flexibility coefficient are NOT expressed by a numerical value but are factors to be taken into consideration when discussing the expansion amount. However, the element Lsin is expressed as a numerical value and serves as the basis of the expansion amount. Here, I'll draw a right triangle. You probably learned in junior high school that in a right triangle with an angle is expressed as a numerical value and serves as the basis of the expansion amount. Here, I'll draw a right triangle. You probably learned in junior high school that in a right triangle with an angle  = 30°, the length of the opposite side of the angle = 30°, the length of the opposite side of the angle is 1/2 of the hypotenuse, or that when the hypotenuse of a right triangle is L and the opposite side of angle ? is a, the sine of angle is 1/2 of the hypotenuse, or that when the hypotenuse of a right triangle is L and the opposite side of angle ? is a, the sine of angle  is denoted by a/L. It's important to remember this. is denoted by a/L. It's important to remember this. |
| How does such a trigonometric function work in calculating the expansion amount? | |
| Tsuchida: | Say this green right triangle as it is, is "the web's left end portion" on an FE roll. To make it easier to visualize, this illustration is extremely enlarged, but the actual angle  is about 1°~3°. Also, think of point O is the inlet point of the web's left end to the FE roll, while point P is the outlet point of the web's left end from the FE roll. So, you can picture side b of the right triangle as the line formed by a web which is supposed to have traveled unexpanded over the FE roll, and hypotenuse L as the line formed by an expanded or inclined web due to FE roll inclination angle is about 1°~3°. Also, think of point O is the inlet point of the web's left end to the FE roll, while point P is the outlet point of the web's left end from the FE roll. So, you can picture side b of the right triangle as the line formed by a web which is supposed to have traveled unexpanded over the FE roll, and hypotenuse L as the line formed by an expanded or inclined web due to FE roll inclination angle  . . |
I see. The hypotenuse L shifts leftward at point P by a distance corresponding to side a due to angle  . Does this mean that the web is expanded on an FE roll by an amount a? . Does this mean that the web is expanded on an FE roll by an amount a? |
|
| Tsuchida: | You bet it is. " The sine of the angle  is denoted by a/L" is expressed in the formula of Sin is denoted by a/L" is expressed in the formula of Sin = a/L. Accordingly, the expansion amount a can be obtained by the formula a = Lsin = a/L. Accordingly, the expansion amount a can be obtained by the formula a = Lsin . More specifically, when theoretically discussing the expansion amount of an FE roll, each of the web's left and right end portions on the FE roll is supposed to be a right triangle. Then, the trigonometric function Sin . More specifically, when theoretically discussing the expansion amount of an FE roll, each of the web's left and right end portions on the FE roll is supposed to be a right triangle. Then, the trigonometric function Sin =a/L is applied to the right triangle and "a = Lsin =a/L is applied to the right triangle and "a = Lsin " is calculated. That is, the expansion amount a of the web's left end portion in the form of a right triangle is obtained by multiplying the hypotenuse L by the antilogarithm of sin " is calculated. That is, the expansion amount a of the web's left end portion in the form of a right triangle is obtained by multiplying the hypotenuse L by the antilogarithm of sin . . |
Sorry, how can I get the antilogarithm of sin ? ? |
|
| Tsuchida: | You can use the established numerical values calculated for sin0° ~ sin45°. Even people not very familiar with mathematics know that the antilogarithm of sin30° is 0.5, as well as the fact that the circle ratio is 3.14. Here, I have only talked about the web's left end portion, but this is also applied to the web's right end portion. Therefore, in the theoretical formula, calculations are made for both the web's left and right end portions with a "2" placed before the parenthesis [  ]. ]. |
I think I get the general idea of Lsin . However, an FE roll is cylindrical. So, the part L is not a straight line, as shown in the illustration, but a curved one, isn't it? . However, an FE roll is cylindrical. So, the part L is not a straight line, as shown in the illustration, but a curved one, isn't it? |
|
| Tsuchida: | Quite so. Since the web is "wound" on an FE roll, a web's end portion does not form a plane right angle as illustrated. Now, I will show you why I have explained this two-dimensionally.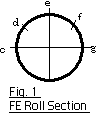 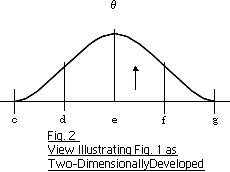 An FE roll section is shown in Fig. 1. The points c - g show respective positions on the roll's circumference. Fig. 2 shows the two-dimensional FE roll circumference. In Fig. 2, the ordinate axis shows a roll inclination angle  while the abscissas axis shows the roll's circumferential positions. In other words, Fig. 2 graphically shows the roll inclination angles while the abscissas axis shows the roll's circumferential positions. In other words, Fig. 2 graphically shows the roll inclination angles  of the respective positions on the roll circumference. It is understood from Fig. 2 that the angle of the respective positions on the roll circumference. It is understood from Fig. 2 that the angle  is not constant, but varies dependent on the respective positions on the roll circumference. At position c, where the rubber cords have maximum contraction, is not constant, but varies dependent on the respective positions on the roll circumference. At position c, where the rubber cords have maximum contraction,  is around 0°, at position e, where there is medium expansion/contraction of the rubber cords, is around 0°, at position e, where there is medium expansion/contraction of the rubber cords,  is the largest, and at position g, where the rubber cords have been stretched to their maximum, is the largest, and at position g, where the rubber cords have been stretched to their maximum,  is again around 0°. is again around 0°. |
Just a moment. The inclination angle  given to an FE roll by its adjusting bolts is not constant for the FE roll in its entirety, but varies dependent on the respective positions of the FE roll, right? given to an FE roll by its adjusting bolts is not constant for the FE roll in its entirety, but varies dependent on the respective positions of the FE roll, right? |
|
| Tsuchida: | Yes. Strictly speaking,  varies continuously on the FE roll's circumference, in the form of a curve, as shown in Fig. 2. More specifically, this curve is a cos curve. For example, when a web is wound on an FE roll circumference at 90° from position d to position f, the angle varies continuously on the FE roll's circumference, in the form of a curve, as shown in Fig. 2. More specifically, this curve is a cos curve. For example, when a web is wound on an FE roll circumference at 90° from position d to position f, the angle on the FE roll circumference varies according to the following formula: on the FE roll circumference varies according to the following formula: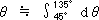 (wherein 45° and 135° are angular expressions of positions d and f.) Accordingly, if I give an explanation in line with actual operation or if I give an explanation of individual expansion amounts for all varying  , it would be very complicated and confusing. So, the expansion amount is now considered on inclination angle , it would be very complicated and confusing. So, the expansion amount is now considered on inclination angle  at position e, where there is medium expansion/contraction of the rubber cords. Please note that at position e, where there is medium expansion/contraction of the rubber cords. Please note that  in the right angle shown above, is the angle in the right angle shown above, is the angle  at position e. As for angle at position e. As for angle  , there are other various points preferably taken into consideration. To simplify this for easier understanding, however, I am now explaining in an "absolutely extremely simplified" form. , there are other various points preferably taken into consideration. To simplify this for easier understanding, however, I am now explaining in an "absolutely extremely simplified" form. |
All right. I welcome this simplified explanation. But, it's still a bit tiring to keep up with. At this time, it's sufficient to understand that expansion a is basically calculated by Lsin , and the rest will be told next time. , and the rest will be told next time. |
